Solving Sudoku with SQL

One thing you are almost guaranteed to see on trains these days is at least one person (quite often more) with pencil poised, glassy-eyed, intensely focused on a Sudoku puzzle. These fascinating numbers puzzles have become exceedingly popular in the UK (and goodness knows where else).

I have never been a keen puzzles enthusiast, so I was initially reluctant to check out this new craze. But seeing how people seemed to be enjoying it I finally gave it a go. I found that it was quite easy to understand the rules, get started, and get stuck in! And soon, before I knew what hit me, I was hooked.

You can think of a Sudoku as a square divided into 9 equal squares (blocks) and the 9 squares each further divided into 9 much smaller squares (cells). That makes 9 blocks and 81 cells (see Figure 1).

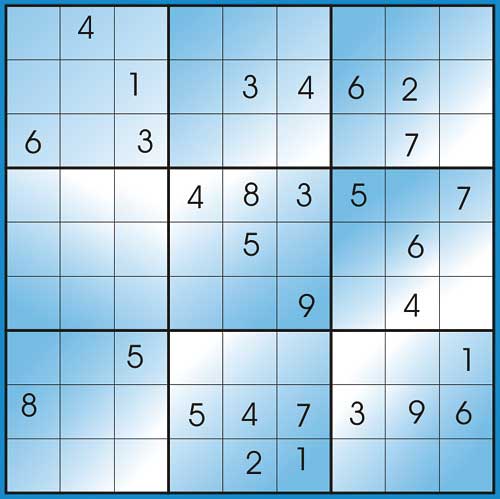
Figure 1: An example of a Sudoku puzzle

The blocks make a 3 x 3 grid (i.e. 3 rows and 3 columns). The cells make a 9 x 9 grid (i.e. 9 rows and 9 columns).

A Sudoku puzzle comes with numbers already present in some of the cells. The objective of the puzzle is to fill in the remaining cells with the right numbers. The cells must be filled according to the following simple rules:

1. All the 9 cells in each row must have the numbers 1 to 9 with no repetition.
2. All the 9 cells in each column must have the numbers 1 to 9 with no repetition.
3. All the 9 cells within each block must have the numbers 1 to 9 with no repetition.

(‘No repetition’ is purely for emphasis, because if you use all of 1 to 9, and you have only 9 places to fill, there can be no repetition anyway.)

Sudoku comes in varying levels of difficulty and degrees of challenge, depending on which, and how many, cells have been filled in already. Whatever the case, you do not need any kind of serious mathematics or clever mental gymnastics; all you need is your own personal logical reasoning and a determination not to be beaten. That is why they can be so much fun.

To make it even more fun for myself, I embarked on an exercise to write a program that solves Sudoku puzzles. And to make it even more challenging I decided not to write the program in the popular object-oriented fashion (Java, C++, C#, etc.) or in any of the old-fashioned procedural programming languages (Pascal, C, Basic etc); but in Transact SQL, within SQL Server 2000. Basically, I wanted to see how the features of T-SQL can be used to develop something like a Sudoku puzzle solution. I have learnt some useful things from the exercise, which I’m eager to pass on to my fellow programmers.

T-SQL is rich in in-built programming functions and features. Far from being just for holding and manipulating data, T-SQL is a programming language in its own right. Many algorithm-based problems that used to be solved with mainstream procedural or object-oriented languages can now be dealt with completely within SQL Server using T-SQL, because not only does it have the usual programming constructs such as ‘While…End’; ‘Case’ and ‘Ifs’; it also, of course, has SQL.

This exercise gave me a chance to use the following programming features of T-SQL:

1. Stored Procedures
2. Tables
3. String manipulation functions
4. ‘While…End’
5. Case statements
6. Temporary tables
7. SQL GROUP BY statements
8. Sub queries

… and probably more.

How the program works

There is no fancy user user-interface. The final program is just one single Stored Procedure called pSolveSudoku. To use it you will need the SQL Analyzer which is the place in SQL Server where SQL queries and stored procedures are run. The example below shows how the stored procedure is used:

The puzzle in Figure 1 is expressed as:

EXEC pSolveSudoku
‘
040000000
001034620
603000070
000483507
000050060
000009040
005000001
800547396
000021000
‘

As you can see, the stored procedure takes a single parameter which is a string, in which there is a number for each cell. The numbers 1 to 9 are used where the values are already known and 0 is used otherwise. It is a good thing that the SQL Query Analyzer interface allows multiple lines to be used in strings otherwise we would have had to write the entire string on a single line, like this:

EXEC pSolveSudoku
‘0400000000010346206030000700004835070
00050060000009040005000001800547396000
021000’

… which is still okay, but not quite as user-friendly.

When you run the stored procedure you get a table showing all the numbers in their right places (see Figure 2) – a solved Sudoku.

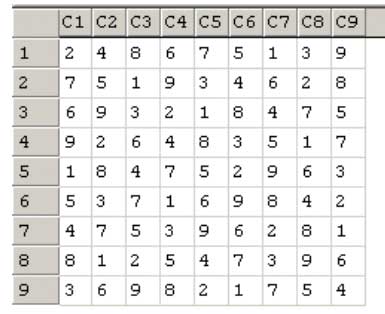
Figure 2: Solution

This information actually comes from a table called tSudoku9x9 which is generated by pSolveSudoku. If you run the following SQL you will get the result of the last puzzle done by the stored procedure.

SELECT * FROM tSudoku9x9

The structure of the table is shown in the table below.

Table 1: The table structure for tSudoku9x9
Column	Data type	Description
R	Integer	Row number
C1	Integer	Column 1
C2	Integer	Column 2
C3	Integer	Column 3
C4	Integer	Column 4
C5	Integer	Column 5
C6	Integer	Column 6
C7	Integer	Column 7
C8	Integer	Column 8
C9	Integer	Column 9

Method

So how does the stored procedure solve the Sudoku?

First let me introduce you to tSudokuData, the most important object in this project. tSudokuData is a table that is populated with all the necessary data which can be queried and updated by stored procedures that automate the task of solving the Sudoku.

tSudokuData contains 81 records, each relating to a cell in the Sudoku. Each record comprises of Location (i.e. row and column number); block information in relation to the cell; ‘Elimination String’ and Current number in the cell.

The ‘Elimination String’ is a special 9-charcter field normally containing ‘123456789’. In the process of solving the puzzle each character is replaced with X when a number has been eliminated from those that can be in the cell. This means that for a cell for which the number is already known the elimination string is ‘XXXXXXXXX’.

The structure of tSudokuData is shown in the table below.

Table 2: The table structure for tSudokuData
Column	Data type	Description
iRow	integer	Row number of the cell (1 to 9)
iCol	integer	column number of the cell (1 to 9)
iVal	integer	the number in the cell 0 for unsolved 1 to 9 for solved
sElim	char(9)	9-character string ‘123456789’, assigned to each cell, in which each character is replaced with X when it has been eliminated from possible numbers that may be used to fill the square
iBlock	integer	Block number (Each block is assigned a number from 1 to 9)
iBRow	integer	Block row (i.e. the row number of the block in the 3X3 grid)
iBCol	integer	Block column (i.e. the column number of the block in the 3X3 grid)
iPos	integer	Within each block the cells are numbered 1 to 9. iPos is the position of the cell within its block.

To populate the table tSudokuData we use the pLoadSudoku Stored Procedure. This does minimal validation on the input string; sets up all the necessary information for each cell, including the elimination string; and assigns values to the cells.

CREATE PROC pLoadSudokuData
	@sInputData VARCHAR(180)
AS
BEGIN
delete tSudokuData
--Remove non-numeric characters from
--the string
--Check that there are 81 characters
declare @i INT
select @i =999
while @i > 0
begin
	SELECT @i = patindex(
		‘%[^0-9]%’,@sInputData)
	SELECT @sInputData =
		replace(@sInputData,substring(
		@sInputData,@i,1),’’)
end
IF len(@sInputData) <> 81
BEGIN
	PRINT ‘Invalid input’
	RETURN
END

DECLARE 	@iRow INT,
	@iCol INT,
	@iVal INT,
	@iBlock INT,
	@iBRow INT,
	@iBCol INT,
	@sElim VARCHAR(9),
	@iPos INT

DECLARE 	@r INT, @c INT
SELECT @r = 1
WHILE @r <= 9
BEGIN
	SELECT @c = 1
	WHILE @c <= 9
	BEGIN
	SELECT
		@iRow =@r,
		@iCol =@c,
		@iVal =
			substring(@sInputData,
			@c+(@r-1)*9,1),
			@sElim =’123456789’,
			@iBlock =CASE
WHEN @r IN (1,2,3) AND @c IN (1,2,3)
	THEN 1
WHEN @r IN (1,2,3) AND @c IN (4,5,6)
	THEN 2
WHEN @r IN (1,2,3) AND @c IN (7,8,9)
	THEN 3
WHEN @r IN (4,5,6) AND @c IN (1,2,3)
	THEN 4
WHEN @r IN (4,5,6) AND @c IN (4,5,6)
	THEN 5
WHEN @r IN (4,5,6) AND @c IN (7,8,9)
	THEN 6
WHEN @r IN (7,8,9) AND @c IN (1,2,3)
	THEN 7
WHEN @r IN (7,8,9) AND @c IN (4,5,6)
	THEN 8
WHEN @r IN (7,8,9) AND @c IN (7,8,9)
	THEN 9
	END,
	@iPos = CASE
WHEN @r IN (1,4,7) AND @c IN (1,4,7)
	THEN 1
WHEN @r IN (1,4,7) AND @c IN (2,5,8)
	THEN 2
WHEN @r IN (1,4,7) AND @c IN (3,6,9)
	THEN 3
WHEN @r IN (2,5,8) AND @c IN (1,4,7)
		THEN 4
WHEN @r IN (2,5,8) AND @c IN (2,5,8)
	THEN 5
WHEN @r IN (2,5,8) AND @c IN (3,6,9)
	THEN 6
WHEN @r IN (3,6,9) AND @c IN (1,4,7)
	THEN 7
WHEN @r IN (3,6,9) AND @c IN (2,5,8)
	THEN 8
WHEN @r IN (3,6,9) AND @c IN (3,6,9)
	THEN 9
END
	SELECT
	@iBRow =CASE
		WHEN @iBlock = 1 THEN 1
		WHEN @iBlock = 2 THEN 1
		WHEN @iBlock = 3 THEN 1
		WHEN @iBlock = 4 THEN 2
		WHEN @iBlock = 5 THEN 2
		WHEN @iBlock = 6 THEN 2
		WHEN @iBlock = 7 THEN 3
		WHEN @iBlock = 8 THEN 3
		WHEN @iBlock = 9 THEN 3
	END,
	@iBCol =CASE
		WHEN @iBlock = 1 THEN 1
		WHEN @iBlock = 2 THEN 2
		WHEN @iBlock = 3 THEN 3
		WHEN @iBlock = 4 THEN 1
		WHEN @iBlock = 5 THEN 2
		WHEN @iBlock = 6 THEN 3
		WHEN @iBlock = 7 THEN 1
		WHEN @iBlock = 8 THEN 2
		WHEN @iBlock = 9 THEN 3
	END

	INSERT tSudokuData(
		iRow,iCol,iBlock,iBRow,iBCol,
			iVal,sElim,iPos)
	VALUES (@iRow,@iCol,@iBlock,
	@iBRow,@iBCol,@iVal,@sElim,@iPos)

	SELECT @c = @c + 1
	END
	SELECT @r = @r + 1
END
UPDATE tSudokuData SET 
	sElim =’xxxxxxxxx’ WHERE iVal != 0
END
GO

Once the table tSudokuData has been created and all the initial information has been inserted into it with pLoadSudokuData, the stage is set for using SQL to solve the Sudoku.

Processing Rules

Most Sudoku fans use a set of rules to place the correct numbers in the cells, in a step-by-step fashion. I can see two kinds of rules:

1. Rules of elimination i.e. finding which number cannot be placed in a cell.
2. Rules of determination i.e. finding which number can be placed in a cell.

Generally I have found that when solving a Sudoku, elimination and determination go hand in hand. A process of elimination often facilitates a process of determination, and vice versa. The ultimate aim is to determine the right number for each cell, but some elimination will have to be done in order to arrive at the right answer.

Elimination

Basic elimination rule: For each cell, look for any number that already exists in the row, column or block that the cell is contained in. If you find such a number, update the elimination string for that cell.

What you do here is to set a number in the elimination string to ‘X’ once you can tell that the number cannot be placed in the cell because it has already been used in the block, the row or the column that the cell is part of. The Stored procedure for this process is pBasicElimination, and it is shown below:

CREATE PROC pBasicElimination
AS
	DECLARE
		@myRow INT,
		@myCol INT,
		@myBlock INT,
		@myPosInBlock INT,
		@myelimStr varchar(9),
		@iCurrentVal INT

	SELECT @myRow=1
	WHILE @myRow <=9
	BEGIN
		SELECT @myCol=1
		WHILE @myCol <=9
		BEGIN
			SELECT
			@myBlock =iBlock,
			@myPosInBlock =iPos,
			@myelimStr =sElim
			FROM tSudokuData
			WHERE
				iRow = @myRow
				AND iCol = @myCol

			SELECT @iCurrentVal = 1
			WHILE @iCurrentVal <=9
			BEGIN
				SELECT @myelimStr =
				CASE
				WHEN
				-- Along the row
				EXISTS(SELECT 1
					FROM tSudokuData
					WHERE iRow=@myRow
					AND iVal =
					@iCurrentVal AND
					iCol != @myCol)
					OR
				-- Along the column
				EXISTS(SELECT 1 FROM
					tSudokuData
					WHERE iCol=@myCol
					AND iVal =
					@iCurrentVal AND iRow
					!= @myRow)
					OR
				-- Within the Block
				EXISTS(SELECT 1 FROM
					tSudokuData
					WHERE iBlock=@myBlock
					AND iVal =
					@iCurrentVal AND iPos
					!= @myPosInBlock)
			THEN replace(
			@myelimStr,@iCurrentVal,’X’)
			ELSE @myelimStr
		END

		UPDATE
		tSudokuData
		SET sElim = @myelimStr
		WHERE
			iRow = @myRow
			AND iCol = @myCol

		SELECT @iCurrentVal =
			@iCurrentVal + 1
		END -- @iCurrentVal
		SELECT @myCol = @myCol + 1
		END -- @myCol
		SELECT @myRow = @myRow + 1
		END -- @myRow
GO

Three things to note: first we have used a while loop to access each cell in the block using the variables @myRow and @myCol; then we have tested for existence numbers 1 to 9 in each row, column or block accordingly using the variable @iCurrentVal; and finally, we have used the replace function to set the numbers that we found in the elimination string to X.

Secondary elimination rule: This rule can be applied if some elimination has already been carried out and it can be stated as: if there is a row, column or block in which two of the cells have both been eliminated down to the same 2 numbers, then those numbers can be eliminated from other cells in the same row column or block.

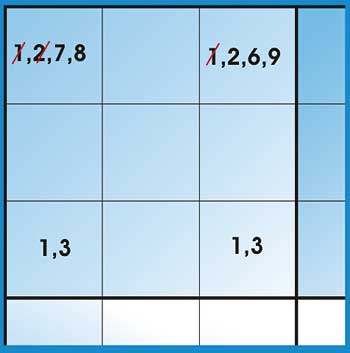
Figure 3: Two cells eliminated

In the example in Figure 3 we are looking at a block in which 2 cells have been eliminated down to 1 and 3. A third cell has been eliminated down to 1, 3, 7 and 8; and a fourth down to 1, 2, 6 and 9. According to this rule we can eliminate the 1 and 3 in the third and fourth cell.

The stored procedure that deals with this process is pSecondaryElimination which comprises of pSecondaryElimByRow, pSecondaryElimByColumn and pSecondaryElimByBlock. As you can imagine, the three component stored procedures are quite similar, so I will only explain pSecondaryElimRow here.

CREATE Proc pSecondaryElimByRow
AS
BEGIN
-- 1. Get a list of all cells in
-- columns where there are n1,n2
select *, remainingNums =
		replace(sElim,’X’,’’),
		matchedN1N2 = convert(varchar(9), null)
into #tmp
from tSudokuData t0
where
exists
(
	select iRow,replace(sElim,’X’,’’),
	count(*) from tSudokuData t1
	where len(replace(sElim,’X’,’’))=2
	and t0.iRow=t1.iRow
	group by iRow,replace(sElim,’X’,’’)
	having count(*) = 2
)
order by iRow

-- 2. Get the only the cells that have the matched n1,n2
select iRow,remainingnums,icount=count(*)
into #tmpMatches
from #tmp
where len(replace(sElim,’X’,’’)) = 2
group by iRow,remainingnums
having count(*) = 2

-- 3. Assign the matched n1,n2 to all 
-- the columns concerned
update #tmp
set matchedN1N2=t2.remainingnums
from
	#tmp t1,
	#tmpMatches t2
where
	t1.iRow = t2.iRow

-- 4. update tSudokuData elimination strings
update
	tSudokuData
set
	sElim= replace(replace(tm.sElim,substring(
	tm.matchedN1N2,1,1),’X’),
	substring(tm.matchedN1N2,2,1),’X’)
from #tmp tm, tSudokuData ts
where tm.iRow=ts.iRow
and tm.iCol=ts.iCol
and tm.matchedN1N2 != tm.remainingnums
END
GO

Here we have used temporary tables to hold data as we have gone through the steps required to implement the rule. ‘Exists’, Sub queries and ‘Group By’ have featured in the complex SQL statements. But the code is concise and it is broken down into identifiable stages.

Determination

Basic determination rule: determine for each cell whether there is a number that is the only one that has not been used in the row, column or block to which the cell belongs. If you find such a number then fill the cell with it.

For example, you are looking at a row and you find that it already contains 1, 2, 3, 5,6,7,8 and 9. One cell has not yet been filled. Easy – the missing number is 4, so fill that in.

Since we will be running the Basic elimination Stored procedure first, the elimination string for this cell will be a series of Xs with only one number. i.e. xxx4xxxxx

To fill in all the cells throughout the whole solution, where all the possible candidate numbers have been eliminated down to ‘4’ we use the following SQL:

UPDATE tSudokuData SET iVal=4,
	sElim=’XXXXXXXXX’
	WHERE sElim =’XXX4XXXXX’

The stored procedure pBasicDetermination, which deals with this rule, is the simplest of all the stored procedures:

CREATE PROC pBasicDetermination
AS
BEGIN
UPDATE tSudokuData SET iVal=1,
	sElim=’XXXXXXXXX’
	WHERE sElim =’1XXXXXXXX’
UPDATE tSudokuData SET iVal=2,
	sElim=’XXXXXXXXX’
	WHERE sElim =’X2XXXXXXX’
UPDATE tSudokuData SET iVal=3,
	sElim=’XXXXXXXXX’
	WHERE sElim =’XX3XXXXXX’
UPDATE tSudokuData SET iVal=4,
	sElim=’XXXXXXXXX’
	WHERE sElim =’XXX4XXXXX’
UPDATE tSudokuData SET iVal=5,
	sElim=’XXXXXXXXX’
	WHERE sElim =’XXXX5XXXX’
UPDATE tSudokuData SET iVal=6,
	sElim=’XXXXXXXXX’
	WHERE sElim =’XXXXX6XXX’
UPDATE tSudokuData SET iVal=7,
	sElim=’XXXXXXXXX’
	WHERE sElim =’XXXXXX7XX’
UPDATE tSudokuData SET iVal=8,
	sElim=’XXXXXXXXX’
	WHERE sElim =’XXXXXXX8X’
UPDATE tSudokuData SET iVal=9,
	sElim=’XXXXXXXXX’
	WHERE sElim =’XXXXXXXX9’
END
GO

For most puzzles marked as ‘easy’ in Sudoku puzzle books, the rules discussed so far are normally sufficient to solve them completely, but for harder Sudoku we need more rules.

Secondary determination rule: This method is familiar to seasoned Sudoku fans: Take the 3 blocks along the same row. Look for a number n that is contained in 2 of the blocks but not the third. In the block that does not contain the number n; look at the row of cells other than the rows that contain n in the other 2 blocks. If there is only one un-filled cell in that row then it should be filled with the number n.

If there is more than one un-filled cell then look at the column that contains each of the cells, to see whether n as been used. That way you can work out into which of the un-filled cells to place the number n.

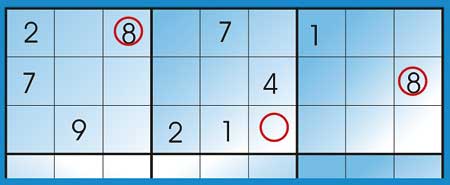
Figure 4: Applying the secondary determination rule

In Figure 4, two blocks have the number 8 in rows 1 and 2 respectively, therefore according to the Secondary determination rule, the middle block, which is the one that does not contain 2, should have 8 in the un-filled cell in row 3.

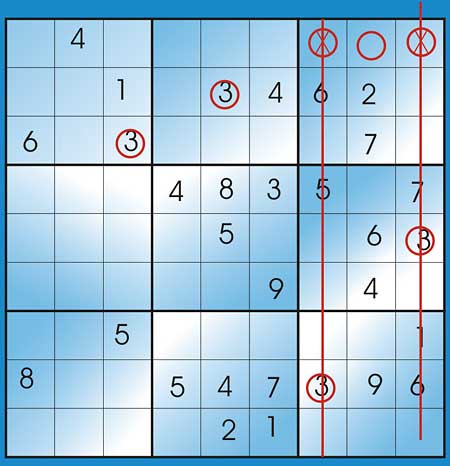
Figure 5: Multiple unfilled cells

Figure 5 shows an example of where more than one unfilled cells have been found. You can see how we have ruled two of them out because ‘3’ has been used in their columns.

This method can also be applied to blocks along the same column, using the same reasoning. The Stored Procedure used for this rule is pSecondaryDetermination and it comprises of pSecondaryDetRowOfBlocks (for blocks in a row) and pSecondaryDetColumnOfBlocks (for column of blocks). Again I will show just one, pSecondaryDetRowOfBlocks:

CREATE PROC pSecondaryDetRowOfBlocks
	@number INT, @blockNumber INT
AS
-- Ensure that n is not currently in 
-- the block
IF (SELECT count(*) FROM tSudokuData
	where iBlock=@blockNumber AND
	iVal=@number) >0
BeGIN
	RETURN
END

-- Determine the Column number of the 
-- block
DECLARE @blockRow INT
SELECT @blockRow = iBRow FROM
	tSudokuData
	WHERE iBlock = @blockNumber

-- Get the cell in the other 2 blocks 
-- with value n
IF (SELECT COUNT(*) FROM tSudokuData
	WHERE iBlock != @blockNumber AND
	iBRow = @blockRow AND iVal=@number)
	< 2
BEGIN
-- n is contained in Only one block
	RETURN
END

-- Get the row in the block that is 
-- not the same as that of cell in the 
-- other 2 blocks with value n
-- And which does not already have a
-- value
SELECT * INTO #tmp FROM tSudokuData
	gm1
WHERE
	NOT iRow IN (SELECT iRow FROM
		tSudokuData
		WHERE iBlock != @blockNumber
		AND iBRow = @blockRow
		AND iVal=@number)
AND iBlock= @blockNumber
AND iVal=0

-- Get the columns that n is not 
-- already contained in the row that 
-- this cell is in
-- How many of the columns already 
-- have n?
DECLARE @CC INT,
	@cntr INT

select @CC=iCol, @cntr=count(
	case when iVal=@number then 1 else
	null end)
from tSudokuData where iCol in (select
	iCol from #tmp) group by iCol
HAVING count(
	case when iVal=@number then 1 else null end) = 0

-- Update tSudokuData
IF @@rowcount = 1
BEGIN
	UPDATE tSudokuData SET iVal=@number, sElim=’XXXXXXXXX’
	FROM #tmp t, tSudokuData g
	WHERE t.iRow=g.iRow AND t.iCol=g.iCol AND t.iCol=@CC
END
GO

As you can see this is the most complex of all the stored procedures, but it is broken down into stages and comments are provided to explain what we are trying to achieve. Also, notice that the stored procedure requires parameters @number (the number we are testing for) and @blockNumber (the block number of the block that we are processing). This means that this stored procedure will be used in a kind of loop where different values will be passed to it. The passing of values happens in pSecondaryDetermination which is given below:

CREATE PROC pSecondaryDetermination
/*
Do a block scan for all the numbers
(1-9) in all the blocks (1-9)
*/
AS
BEGIN
	DECLARE @blockNumber INT, @number INT
	SELECT @blockNumber = 1
	WHILE @blockNumber <= 9
	BEGIN
	SELECT @number = 1
	WHILE @number <= 9
		BEGIN
			EXEC
			pSecondaryDetColumnOfBlocks @blockNumber,@number
			EXEC
			pSecondaryDetRowOfBlocks @blockNumber,@number
			SELECT @number = @number + 1
		END
	SELECT @blockNumber = @blockNumber + 1
	END
END
GO

Putting it all together

The top level stored procedure pSolvesudoku uses the other stored procedures in an iterative manner. These are the steps:

1. Set up the tSudokuTable and load in the input string
2. Find out how many solved cells are in the Sudoku
3. Apply the stored procedures for solving the Sudoku
4. Check the number of solved cells, if still the same, then stop, otherwise go to 3.
5. Indicate whether the Sudoku was completed or not.
6. Display the solution

CREATE PROC pSolveSudoku @sData VARCHAR(1000)
AS
BEGIN
-- 1. Set up the tSudokuTable and load in the data
-- 2. Find out how many solved sudokus
-- 3. Apply the stored procedures for solving the Sudoku
-- 4. Check the number of solved cells, if still the same
-- then stop

Exec pLoadSudokuData @sData

DECLARE @no_of_solved INT, @finished CHAR(1)
SELECT @no_of_solved = count(*) FROM
	tSudokuData WHERE iVal != 0

WHILE 1 =1 -- loop for evermore!
BEGIN
	exec pBasicElimination
	exec pBasicDetermination
-- Apply the elimination string to the puzzle
	exec pSecondaryDetermination
	exec pSecondaryElimination
	exec pBasicDetermination
-- Apply the elimination string to the puzzle
	IF @no_of_solved =(SELECT count(*)
		FROM tSudokuData WHERE iVal != 0)
	BEGIN
		-- No more solutions
		IF @no_of_solved = 81
		BEGIN
			PRINT ‘All Cells have been solved’
		END
		ELSE
		BEGIN
			PRINT ‘Not all Cells have been solved’
		END
	EXEC pShowSudoku
	RETURN
	END
	SELECT @no_of_solved = count(*)
		FROM tSudokuData WHERE iVal != 0
END -- while
	 SELECT @no_of_solved
END
GO

Conclusion

This has been a fun project. It proves that T-SQL is more versatile than you might imagine, and it only gets better with SQL Server 2005.

This exercise is by no means complete. It can be taken further, by adding more rules so that it can solve harder Sudoku. With some adjustment it can also be converted into a Sudoku Puzzle Generator. It can even be further enhanced and converted to a web service using the new features in SQL Server 2005, but that is another story.

---

Samuel Aina is an IT Consultant working mainly for commercial banks and programming in Visual Basic and SQL Server, among other platforms. He is an MIAP (Member of the Institution of Analysts and Programmers).