Functional Cells : A Spreadsheet in F#

Live code is available at https://bitbucket.org/ptrelford/spreadsheet-developerfusion/src

Functional programming is beginning to hit the mainstream in Java and .Net. The Java community has seen significant growth in languages like Clojure and Scala, while the use of LINQ, a feature based heavily on functional programming concepts, in C# and VB.NET is now common place. And of course, Visual Studio 2010 now ships with the F# programming language - the first brand-new “out of the box” language to the .NET ecosystem since its introduction of C# back in 2001.

If you’ve ever written formulas in a spreadsheet then you’re already familiar with some of the principles of functional programming. The key building blocks of a spreadsheet are cells containing functions and values. To demonstrate functional programming at large, this article will be looking at the implementation of a functional spreadsheet written in F# and bound to the DataGrid control, as shown in Figure 1.

Figure 1 : The spreadsheet application running in the browser from http://fssnip.net/4v

There are two parts to this application which we'll look at in turn.

1. A parser to interpret any formula entered into a cell.
2. A simple object model representing the sheets, rows and cell in a spreadsheet.

When we’re happy they are working we can use data binding from a DataGrid to the Object Model to view the cells. For this we can use either WPF or Silverlight.

Pre-Requisites

To follow this article, you’ll need to install F#. If you have a non-Express version of Visual Studio 2010 Professional, you already have F# installed. If not and you run Windows, you can download the Visual Studio 2010 Shell for free and install F# into it. The F# Developer center has the details. If you’re on Linux or Mac then you can use F# with Mono 2.6/2.8 with MonoDevelop or Emacs. You can even edit F# code in your browser here.

Note that should you wish to try out any of the F# code fragments below in Visual Studio, just type the code into an open F# file, highlight it and press ALT + ENTER to have it run inside Visual Studio’s F# Interactive window.

Parsing Formulae In A Spreadsheet Cell

Any cell in a spreadsheet may contain a formula to derive its value from the values of other cells in the spreadsheet instead of a simple value of its own. For example,

• A1+A2
• C1*C5
• 2-1

In order to interpret these formulae correctly, we’ll need to create a parser that:

• Takes a formula and splits it into its component parts: strings, operators, cell references and integers. We'll refer to these collectively as tokens and the process of conversion as tokenization.
• Parses the sequence of tokens to build an Abstract Syntax Tree for the cell’s formula, that can later be evaluated

We’ll look at these in order.

Tokenization

The first step in the tokenization process is to define a set of possible tokens. In addition to the four types mentioned above - strings, operators, cell references and integers - we also include whitespace and single symbol characters ($, % etc) and define the six types using a Discriminated Union. (For C# users, this works like a C# class hierarchy where token is an abstract base class.)

type token =
    | WhiteSpace
    | Symbol of char
    | OpToken of string
    | RefToken of int * int
    | StrToken of string
    | NumToken of decimal

Our object model will reference a cell by column and row numbers, so we'll also need a function to convert cell references, e.g. A1, C3, into column and row numbers. It's called toRef.

let toRef (s:string) =
    let col = int s.[0] - int 'A'
    let row = s.Substring 1 |> int
    col, row-1

With those two items in place, we can use regular expressions to identify the tokens in a formula. To implement this, we'll define an Active Pattern (a function that can be used actively inside a pattern matching expression) for matching regular expressions and a function called toToken to map regular expressions to tokens.

let (|Match|_|) pattern input =
    let m = System.Text.RegularExpressions.Regex.Match(input, pattern)
    if m.Success then Some m.Value else None

let toToken = function
    | Match @"^\s+" s -> s, WhiteSpace
    | Match @"^\+|^\-|^\*|^\/" s -> s, OpToken s
    | Match @"^=|^<>|^<=|^>=|^>|^<" s -> s, OpToken s   
    | Match @"^\(|^\)|^\,|^\:" s -> s, Symbol s.[0]   
    | Match @"^[A-Z]\d+" s -> s, s |> toRef |> RefToken
    | Match @"^[A-Za-z]+" s -> s, StrToken s
    | Match @"^\d+(\.\d+)?|\.\d+" s -> s, s |> decimal |> NumToken
    | _ -> invalidOp ""

Note that toToken only expects to match one prospective token at a time in order to categorize it. So we also need to define a function we'll call tokenize that works through the whole formula string in a cell as input and uses toToken to return a List of tokens:

let tokenize s =
    let rec tokenize' index (s:string) =
        if index = s.Length then [] 
        else
            let next = s.Substring index 
            let text, token = toToken next
            token :: tokenize' (index + text.Length) s
    tokenize' 0 s
    |> List.choose (function WhiteSpace -> None | t -> Some t)

The tokenize function invokes the inner recursive function tokenize’, marked with the rec keyword, before choosing all tokens from the list which are not whitespace. The recursive tokenize’ function repeatedly tries to match the front of the string against a token until the end of the string is reached.

Now we can tokenize a formula, let’s try it in F# interactive. Select all the code written so far and click Alt+Enter. F# interactive will open and you can now call tokenize directly:

> tokenize "C9+10";;
val it : token list = [RefToken (2,8); OpToken "+"; NumToken 10M]

> tokenize "(1+1)=2";;
val it : token list =
  [Symbol '('; NumToken 1M; OpToken "+"; NumToken 1M; Symbol ')'; OpToken "="; NumToken 2M]

Token Parsing

The second half of the formula parser takes the list of tokens, turn them into a formula it can understand and then evaluates it. Just like the tokenization code, we begin by defining the allowed elements of a formula. They are:

• Negation operator
• The arithmetic operators for addition, subtraction, multiplication and division
• The logical comparison operators equal to, less than, greater than, less than or equal to, greater than or equal to, and not equal to.
• A cell reference (as row and column number)
• A range of cells (as row and column numbers specifying the range’s start and end)
• A function being applied to part of the formula.

We can use three discriminated unions to define these elements as follows:

type arithmeticOp = Add | Sub | Mul | Div
type logicalOp = Eq | Lt | Gt | Le | Ge | Ne
type formula =
    | Neg of formula
    | ArithmeticOp of formula * arithmeticOp * formula
    | LogicalOp of formula * logicalOp * formula
    | Num of decimal
    | Ref of int * int
    | Range of int * int * int * int
    | Fun of string * formula list

With these in place, we can combine several mutually recursive functions starting with Term to define a Recursive Descent Parser for each of these operators. The code below shows a cut down version of this which deals with just addition and subtraction along with the parse function which passes the original set of tokens into Term. You can find the other five functions – Factor, Product, Atom, Tuple and Params - within the parser in the code download.

let rec (|Term|_|) = function
    | Number(f1, OpToken "+"::Term(f2,t)) -> Some(ArithmeticOp(f1,Add,f2), t)
    | Number(f,t) -> Some(f,t)
    | _ -> None
and (|Number|_|) = function
    | NumToken(n)::t -> Some(Num(n),t)
    | _ -> None

// Full parser in download

let parse s = 
    tokenize s |> function 
    | Term(e,[]) -> e 
    | _ -> failwith "Failed to parse formula"

Running in F# Interactive:

> parse "1";;
val it : formula = Num 1M
> parse "1+1";;
val it : formula = ArithmeticOp (Num 1M,Add,Num 1M)
> parse "1+1+1";;
val it : formula = ArithmeticOp (Num 1M,Add,ArithmeticOp (Num 1M,Add,Num 1M))

Formula Evaluation

Now we can parse formulae into a format we can act upon and therefore evaluate, we need to write the function that does the evaluation. Happily this is quite straightforward, using a recursive function to work through the list of arithmetic and logical operations tokens and doing the relevant calculation: addition for Add, subtraction for Sub etc.

The following evaluate function computes any specified formula, using a specified valueAt function to resolve the values of other cells:

let evaluate (valueAt:int * int -> string) formula =
    let rec eval = function
        | Neg f -> - (eval f)
        | ArithmeticOp(f1,op,f2) -> arithmetic op (eval f1) (eval f2)
        | LogicalOp(f1,op,f2) -> if logic op (eval f1) (eval f2) then 0.0M else -1.0M
        | Num d -> d
        | Ref(x,y) -> valueAt(x,y) |> decimal
        | Range _ -> invalidOp "Expected in function"
        | Fun("SUM",ps) -> ps |> evalAll |> List.sum
        | Fun("IF",[condition;f1;f2]) -> 
            if (eval condition)=0.0M then eval f1 else eval f2 
        | Fun(_,_) -> failwith "Unknown function"
    and arithmetic = function
        | Add -> (+) | Sub -> (-) | Mul -> (*) | Div -> (/)
    and logic = function         
        | Eq -> (=)  | Ne -> (<>)
        | Lt -> (<)  | Gt -> (>)
        | Le -> (<=) | Ge -> (>=)
    and evalAll ps =
        ps |> List.collect (function            
            | Range(x1,y1,x2,y2) ->
                [for x=x1 to x2 do for y=y1 to y2 do yield valueAt(x,y) |> decimal]
            | x -> [eval x]            
        )
    eval formula

Again we can use F# interactive to test this:

> let eval s = s |> parse |> evaluate (fun (x,y) -> 0);;
val eval : string -> decimal
> eval "1+1";;
val it : decimal = 2M

Finally, in order to propagate changes between cells in a sheet we need to resolve the other cells that a particular formula references:

let references formula =
    let rec traverse = function
        | Ref(x,y) -> [x,y]
        | Range(x1,y1,x2,y2) -> 
            [for x=x1 to x2 do for y=y1 to y2 do yield x,y]
        | Fun(_,ps) -> ps |> List.collect traverse
        | ArithmeticOp(f1,_,f2) | LogicalOp(f1,_,f2) -> 
            traverse f1 @ traverse f2
        | _ -> []
    traverse formula

And in F# interactive:

> Range(1,1,3,1) |> references;;
val it : (int * int) list = [(1, 1); (2, 1); (3, 1)]

The Object Model

A Spreadsheet comprises sheets that are composed from columns and rows. Rows are composed from cells. Finally the cells contain data in the form of either literals or formulas which are in turn evaluated and displayed as values. Or in UML:

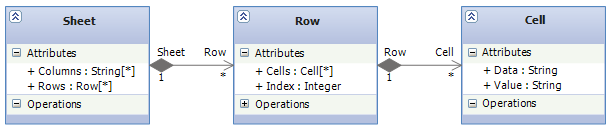
This hierarchy can be expressed using F# classes:

type Cell (x,y) =
    let mutable data = ""
    member cell.Data
        with get () = data
        and  set text = data <- text        
    member cell.Value = data |> parse |> eval

type Row (index,columnCount) =
    let cells = Array.init columnCount (fun x -> Cell(x,index))
    member row.Cells = cells
    member row.Index = index+1

type Sheet (columnCount, rowCount) =    
    let columns = Array.init columnCount (fun i -> ('A' + char i))
    let rows = Array.init rowCount (fun i -> Row(i, columnCount))
    member sheet.Columns = columns
    member sheet.Rows = rows

However this is not enough on its own. When a cell’s value changes all cells that reference that cell must also be updated. To achieve this we can implement an Update event to signal a change to a cell’s value. The following code implements an Updated notification:

type Cell (x,y) =
    let mutable data = ""
    let mutable value = ""
    let updated = Event<_>()    
    member cell.Data
        with get () = data
        and  set text =
            data <- text                
            updated.Trigger value
    member cell.Value = data |> parse |> eval
    member cell.Updated = updated.Publish

Then by using the references function we defined earlier, it is possible for a cell to subscribe to updates from all the cells it references.

The Object Model is defined as a set of mutually recursive types where cells contain both raw text data and an implied value. Dependent cells are notified of updates via the Updated event:

type Cell (sheet:Sheet) as cell =
    inherit ObservableObject()
    let mutable value = ""
    let mutable data = ""       
    let mutable formula : formula option = None
    let updated = Event<_>()
    let mutable subscriptions : System.IDisposable list = []   
    let cellAt(x,y) = 
        let (row : Row) = Array.get sheet.Rows y
        let (cell : Cell) = Array.get row.Cells x
        cell
    let valueAt address = (cellAt address).Value
    let eval formula =         
        try (evaluate valueAt formula).ToString()       
        with _ -> "N/A"
    let parseFormula (text:string) =
        if text.StartsWith "="
        then                
            try true, parse (text.Substring 1) |> Some
            with _ -> true, None
        else false, None
    let update newValue generation =
        if newValue <> value then
            value <- newValue
            updated.Trigger generation
            cell.Notify "Value"
    let unsubscribe () =
        subscriptions |> List.iter (fun d -> d.Dispose())
        subscriptions <- []
    let subscribe formula addresses =
        let remember x = subscriptions <- x :: subscriptions
        for address in addresses do
            let cell' : Cell = cellAt address
            cell'.Updated
            |> Observable.subscribe (fun generation ->   
                if generation < sheet.MaxGeneration then
                    let newValue = eval formula
                    update newValue (generation+1)
            ) |> remember
    member cell.Data 
        with get () = data 
        and set (text:string) =
            data <- text        
            cell.Notify "Data"          
            let isFormula, newFormula = parseFormula text               
            formula <- newFormula
            unsubscribe()
            formula |> Option.iter (fun f -> references f |> subscribe f)
            let newValue =
                match isFormula, formula with           
                | _, Some f -> eval f
                | true, _ -> "N/A"
                | _, None -> text
            update newValue 0
    member cell.Value = value
    member cell.Updated = updated.Publish

Rows are constructed from cells:

and Row (index,colCount,sheet) =
    let cells = Array.init colCount (fun i -> Cell(sheet))
    member row.Cells = cells
    member row.Index = index

Sheets are constructed from of columns rows :

and Sheet (colCount,rowCount) as sheet =
    let cols = Array.init colCount (fun i -> string (int 'A' + i |> char)) 
    let rows = Array.init rowCount (fun index -> Row(index+1,colCount,sheet))  
    member sheet.Columns = cols    
    member sheet.Rows = rows
    member sheet.MaxGeneration = 1000

To signal changes in cells to WPF or Silverlight we implement the INotifyPropertyChanged interface:

and ObservableObject() =
    let propertyChanged = 
        Event()
    member this.Notify name =
        propertyChanged.Trigger(this,PropertyChangedEventArgs name)
    interface INotifyPropertyChanged with
        []
        member this.PropertyChanged = propertyChanged.Publish

Referencing WPF 4.0 Assemblies (64-bit Windows)

Assembly reference can be added to the project, alternatively if you are running with F# interactive they can be specified using the #r directive:

#r @"C:\Program Files (x86)\Reference Assemblies\Microsoft\Framework\.NETFramework\v4.0\PresentationCore.dll"
#r @"C:\Program Files (x86)\Reference Assemblies\Microsoft\Framework\.NETFramework\v4.0\PresentationFramework.dll"
#r @"C:\Program Files (x86)\Reference Assemblies\Microsoft\Framework\.NETFramework\v4.0\System.Xaml.dll"
#r @"C:\Program Files (x86)\Reference Assemblies\Microsoft\Framework\.NETFramework\v4.0\WindowsBase.dll"

Now we can use data binding to show a Sheet on a DataGrid with WPF using Data Binding. First we need a function to create a grid template column that binds to a column’s cells:

open System.Windows
open System.Windows.Controls
open System.Windows.Data
open System.Windows.Markup

let createGridColumn i =
    let header = 'A' + char i
    let col = DataGridTemplateColumn(Header=header, Width=DataGridLength(64.0))
    let toDataTemplate s =
        let ns = "http://schemas.microsoft.com/winfx/2006/xaml/presentation"
        sprintf "%s" ns s
        |> XamlReader.Parse :?> DataTemplate
    let path = sprintf "Cells.[%d]" i
    col.CellTemplate <- 
        sprintf "" path
        |> toDataTemplate
    col.CellEditingTemplate <- 
        sprintf "" path
        |> toDataTemplate
    col

Next we need a function to create the grid and bind the sheet’s column’s and rows to it:

let createGrid (sheet:Sheet) =
    let grid = DataGrid(AutoGenerateColumns=false,HeadersVisibility=DataGridHeadersVisibility.All)
    for i = 0 to sheet.ColCount-1 do createGridColumn i |> grid.Columns.Add
    grid.LoadingRow.Add (fun e ->
        let row = e.Row.DataContext :?> Row
        e.Row.Header <- row.Index
    )
    grid.ItemsSource <- sheet.Rows
    grid

Finally we create a sheet and a Window, setting the content of the window as a grid bound to the sheet:

let sheet = Sheet(26,30)
let win = new Window(Title="Spreadsheet", Content=createGrid sheet)
do  win.ShowDialog()

When you run the code you should now see a functioning Spreadsheet:

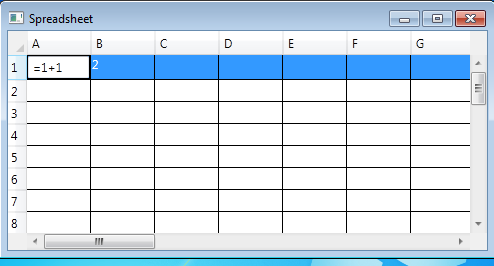
What Next?

Why not try extending the Spreadsheet script with:

• your own functions (inside the evaluate function)
• support for Dates and Times
• or even units of measure
• support for copy and paste to and from Excel
• or even support import and export of Excel files

To see features like these implemented checkout the Cellz project on CodePlex.

Read more about Functional Programming in .Net with Real-World Functional Programming with examples in C# & F#